Fun with Picture Grids: Teaching Multiplication of Fractions & Decimals
Order a set at: http://www.hand2mind.com/catalog/product?deptId=&prodId=020272&q=picture+grids This is the third and fourth parts of the Fun with Picture Grids Series of Addition, Subtraction, Division, Multiplication & Decimals, and Square RootPart III: Teaching Multiplication with the Picture Grids Manipulatives
A few weeks later Henry asks the class, “How do you feel about multiplication?” The students groan. Multiplication is even harder than addition and subtraction. They’re not ready to believe that these grids hold the magic that can ease the discomfort of multiplication. After all, students rarely find “magic” in the classroom. “How many of you believe in magic?” Henry asks. Only a few hands go up. Henry knows that these few hands belong to courageous students; those brave enough to confess they still believe in magic are most likely the ones in the greatest need of help. “Well,” he says, “I hope more of you will feel differently once we’ve explored multiplication with the grids. And remember, magic means different things to different people. Each one of you would probably have a unique answer to the question. In math, however, there’s only one right answer. The magic is that there are different approaches possible to reach that answer.” The students lean forward in their seats.
Henry takes out the thirds grid and the fourths grid. He holds them up for the students to see. “All right,” he says, “let’s say that we want to take a third of a quarter. What does that mean?” A student replies, “If we divide the quarter into thirds, we could get three equal parts.” Henry answers, “Yes, but what is each of those parts called?”
He asks the students to break into their cooperative learning groups and to then begin to manipulate the grids. Eventually, one student rotates the third grid and slides it across the quarters grid. “I think I’m on to something!” she calls out. Henry smiles. She is the student who groaned the loudest when he announced they would be working on multiplication. “Let’s have a look,” he says. The student has slid the thirds grid entirely across the quarters grid and divided the whole section into twelfths.
Illustration:
1/3 ¼ slide the 1/3 across the ¼
The intersection shows 1/12th
“What have we here?” Henry asks. “There are twelve squares now,” she says. “And what do we call those squares?” he asks. “Twelfths,” the students respond in chorus. Henry turns to another student. “Can you describe what just took place?” he asks. Several other students are eagerly waving -their hands. “Just give him another moment,” Henry says. The boy studies the grids and smiles. “Well, we took one part out of the three parts that make up the quarter.” He thinks for another moment. “I guess now we know that one-third of one quarter is equal to one-twelfth!” Henry applauds, and the students join in. “Excellent work,” Henry says. “I’m impressed.”
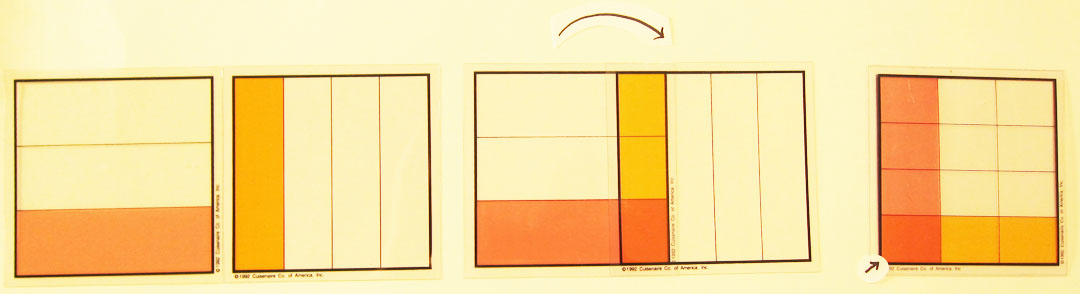
Henry walks over to another group. “Try using the grids to divide a quarters grid into three equal parts.” The students experiment with the different clear grids. “How about the tenths grid?” one girl asks. “Does that give you three equal parts?” Henry says. “I guess not,” she replies. “Try another one,” Henry encourages. “The twelfths grid,” another student says. He and his partner have slid the clear twelfths grid over the quarters grid and divided it into three equal sections.
Illustration:
¼ slides clear 12th over it = 3/12 so one bar = 1/12
“What are each of these three divisions called?” Henry asks. “A twelfth,” the students respond. “Good,” he says. “Now state the problem.” In unison, the students say, “One-third of a quarter equals one-twelfth,” Finally, they prove their conclusion by placing the clear twelfths grid on top of the quarters grid. At the end of the lesson, Henry brings the class together to share and chart their findings.
Part IV: Teaching Decimals with the Picture Grids Manipulatives
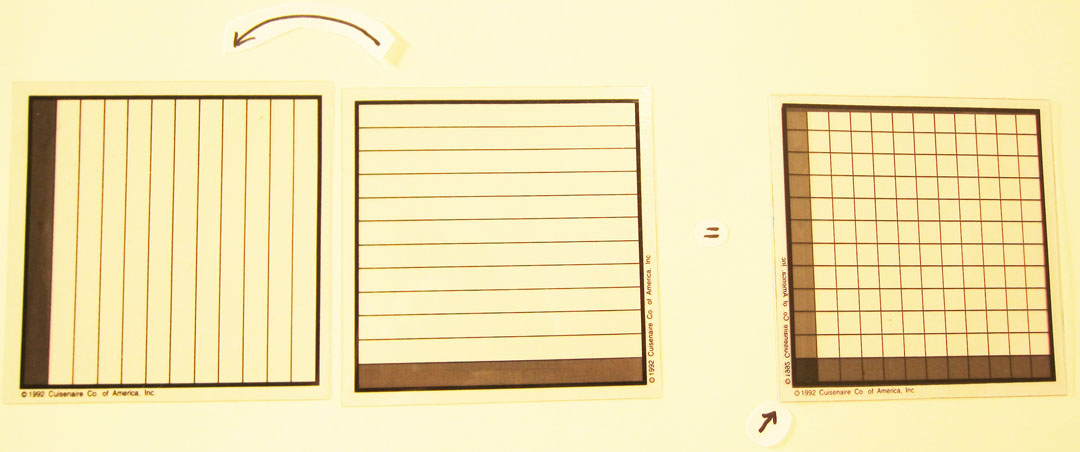
“We can also use the tenths grids to examine decimals,” Henry says. “Let’s say we want to figure out what a tenth of a tenth is equal to. Now that you’ve had the opportunity to work out fractions, let’s see what you can do with decimals. Henry actively listens as he roams from group to group. One student says, “First take a tenths grid. Now take another tenths grid and place it on top of the first tenths grid in the opposite direction.” Another student jumps in with her conclusion. “This divides the bottom tenths grid into ten equal pieces.” Henry smiles. “Well, does that mean we should call each section a hundredth?” The class choruses their approval. “Looks like we have an answer!” Henry says.
Illustration:
1/10 X 1/10 = 1/100
Another group discusses the same concept and Henry poses the question, “If we slide the top grid completely over the bottom grid, we divide the entire area of the square into equal sections. Since there are one hundred divisions, each division is considered a hundredth. So what do we call the fractional part of a tenth?” The students take a few moments to adjust their grids and to consider the question. The answer is right in front of them. “A tenth of a tenth is equal to a hundredth” one student says, and everyone agrees.
At this point, students are encouraged to create their own scenarios with the grids to practice. With repetition, they get the hang of it. Then, Henry asks them to write one of their scenarios along with the diagrams in their Pic-Jour Math journal. Not until Henry is convinced that the pictures/diagrams are strongly linked to the numbers, does Henry move them away from the manipulatives and just use numbers in his teaching practices.
Whether it’s addition, subtraction, multiplication, or decimals, Picture Grids are an invaluable teaching tool. The grids allow teachers to simplify these concepts. The students can actually maneuver the grids and easily see the reasons for their answers. In this way, the students develop a visual understanding of how numbers are used. Then, and only then, do numbers become real and tangible, rather than a meaningless collection of symbols on a page.
There are various ways that students can explain the multiplication and division of fractions.
Please continue onto the next section in the series: Teaching Square Root
Andi Stix is an educational consultant & coach who specializes in differentiation, interactive learning, writing across the curriculum, classroom coaching, and gifted education. For further information on her specialties or social media, please email her on the Contact page.
A Math Manipulative to Teach Fractions and Decimals, © 1993 Speech by Andi Stix, Ed.D.
Association of Mathematics Teachers of New York State, Buffalo, NY, ERIC: Eric Resources Information Center #ED408158 (c) 1992 Picture Grids designed by Andi Stix, Produced by ETA/Cuisenaire Company of America.
References
Schubert, B. (1987). Mathematics journals: Fourth grade. In Toby Fulwiler (Ed.), The Journal Book. (348-358). Portsmouth, NH Boynton/Cook Publishers.
Stix, Andi N. (1992).The Development and Field Testing of a Multi-Modal Method for Teaching Mathematical Concepts to Preservice Teachers by Utilizing Pictorial Journal Writing. Ph.D. diss. Columbia University Teachers College. Ann Arbor, MI: U.M.I. Dissertation Information Service, Pub. #92-18719.
Stix, Andi N. (1994). Pictorial journal writing in mathematics. Arithmetic Teacher, 42:1, 264-269.