Fun with Picture Grids: Teaching the Addition of Fractions
An Introduction to Picture Grids
Why is it that mathematics often conjures up images of desperate students trying to solve seemingly impossible problems? The subject of mathematics often compels otherwise well-adjusted adults to grimace with the memory of futile hours spent poring over numbers that seem at once both meaningless and threatening. Fortunately, there is an alternative. Yes, Virginia, there is a Santa Claus. The impossible really is possible, and we can do more than tell our students to clap their hands and believe
What can we do? I introduce to you Henry Goodman. He is a mathematics teacher. Perhaps, some might even consider him a visionary with an eye toward the coming millennium. Henry Goodman understands that mathematics can be raised to the same level of respect and importance as green leafy vegetables. After all, the children of previous generations balked at the idea of nutritious fruits and veggies. Yet, today we see children reading food labels with the same interest they reserve for studying new Nintendo games. The future is really upon us.
Henry Goodman can offer activities that are appropriate for all levels of students. The materials transcend both developmental age and degree of complexity because they make it possible to understand how mathematics works.
Picture Grids is comprised of sixty different acrylic stained glass window overlays. Each fractional part is represented by a different color: fifths are green, quarters are yellow, thirds are bot pink, and halves are blue. The square grids can be easily maneuvered by both students and teachers. The students need to become familiar with the fractional parts represented by the grids before participating in teacher-developed activities.
We are going to follow Henry Goodman as he shows us how students can visualize math strategies. In addition, he will show us that manipulatives can help clarify process as students learn various ways to find solutions. The final outcome is that students will then be able to compute answers by substituting abstract numbers and symbols for the manipulative.
Henry Goodman reminds us that students will always be working cooperatively in pairs. This gives them an opportunity to discuss the problems between themselves and share the application of the manipulative. In addition, after each problem is solved, students are expected to write or draw the solution in their math journals (Stix, 1992). This process bridges the gap between the abstract numbers and the materials. The writing process also aids in long term memory (Shubert, 191) and encourages communication between the teacher and the student. This is especially practical once the inevitability of learning differences is accepted and the need for different modes of instruction recognized (Stix, 1994).
Part I: Teaching Addition with the Picture Grids Manipulatives
Henry Goodman’s challenge is to teach students how to comprehend fractions. How is two-fourths the same as one-half? And why does one-half and one-quarter equal three-fourths? Is it possible to explain these concepts without the use of a common denominator? An emphatic nod from Henry tells us that not only is a common denominator not always necessary to do fractions, but students can have the advantage of actually seeing how fractions work.
Because of the variety of grids, it is always wise to remove the grids that will be used and place the others aside. Today, Henry pulls out the following grids: halves, quarters, thirds, tenths, twelfths, and hundredths.
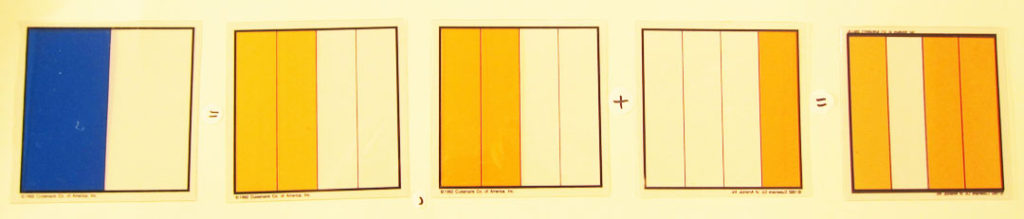
1. Henry uses a quarters picture grid and adds it to a halves picture grid. He asks the class, “How much is one-quarter plus one half?” One group solved this problem by flipping the halves grid on top of the quarters grid and counting the number of quarters created by this combination. It is clear now that one-half plus one-quarter equals three-fourths.
Illustration:
1/4 + ½ = ¾
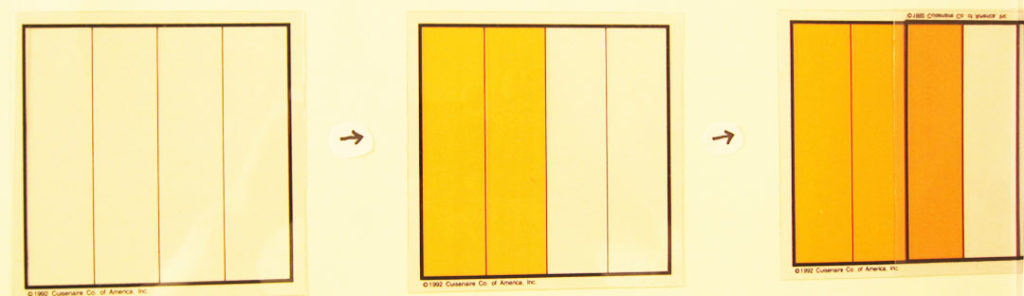
2. He asks another group to return to the original problem of one-quarter plus one-half. He asks the students, “Which of the two grids would you exchange for another grid so you can add them together?” When the students placed the quarter grid on top of the halves grid, they can see the exchange of one-half for two-quarters. They flipped the grids over to prove that they can get three-quarters.
Illustration:
½ = 2/4, 2/4 + ¼ = ¾
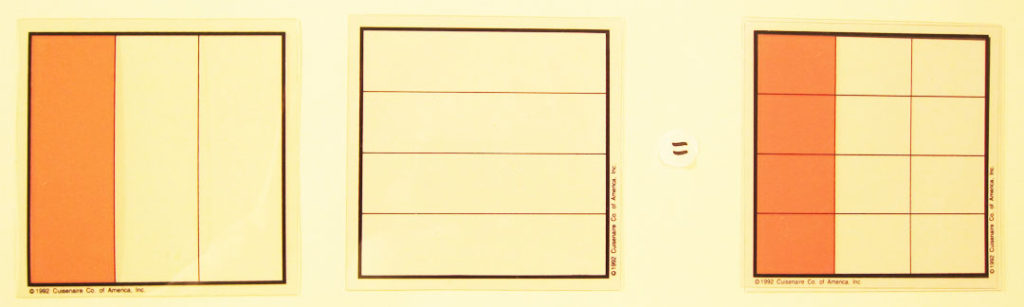
3. As the students continue to use the grids Henry listens to them talk about how grids were exchanged. Henry clarifies how this “exchange” is recognized as the common denominator. A third group stares at the colored wax pencils. Mr. Goodman asks them how they could use the clear grid and pencils to solve the exercise. The group filled in two-quarters with a colored pencil, and then added another quarter.
Illustration:
Clear quarters -> 2/4 -> 2/4/ + ¼ = ¾
4. The following day, Henry takes out the grid that represents thirds and the clear grids that represent fourths and twelfths. At this point, Henry asks each group to use the overhead projector to explain its findings to the rest of the class. He asks the class to “play along” with each teaching group. He gives the grids to the students and asks, “How can you use the clear acetates on top of the colored grids so that each colored section is divided into even parts?” The trick is that each grid must be divided into the same amount of parts. Through discovery learning, some students conclude that the clear grids will have to be rotated sideways in the opposite direction of the colored grids to show the equal parts. Henry asks, “What is the result?” (The students show him the division of twelfths.)
One group solved it like this:
Illustration:
1/3 X clear ¼ = 4/12
“Now,” Henry says, “the fourths grid must also be divided by twelfths.” Once again, through discovery learning, the students see that by rotating the clear thirds grid, twelfths are produced.
Illustration:
¼ X clear 3rds = 3/12
“Look,” Henry says “both acetates have an equal number of squares. This is the original of the common denominator. If we would add them together, how many twelfths would we have?”
One girl says, “If we rotate 4/12ths the inside parts will match each other.”
Illustration:
3/12 + 4/12
The students count to verify that there are 7/12ths altogether.
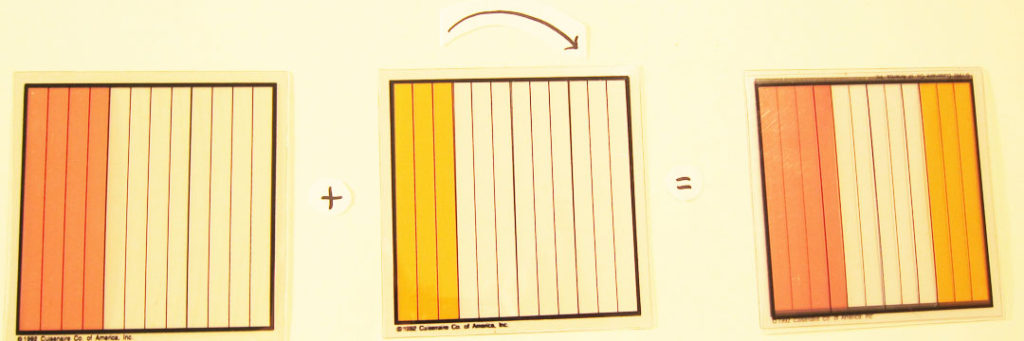
Another group of students develop a completely different system. First, they place the clear twelfths grid on top of the one-thirds grid.
Illustration:
1/3 + clear 12th = 4/12
They then show Mr. Goodman that if they place the twelfths grid on top of the quarter grid, it will equally divide into twelfths.
Illustration:
¼ + clear 12th = 3/12
Next they flip over the 3/12ths grid and place it on top of the 4/12ths grid.
Illustration:
4/12 + 3/12 = 7/12
“Now,” one student says, “we have 7/12ths!”
Henry asks, “What do you think is the meaning of the common denominator?” A student raises his hand and says, “When two fractions have the same size parts.” Henry nods. “What is another way of saying this?” As students answer, he charts their definitions.
At this point, students are encouraged to create their own scenarios with the grids to practice. With repetition, they get the hang of it. Then, Henry asks them to write one of their scenarios along with the diagrams in their Pic-Jour Math journal. Not until Henry is convinced that the pictures/diagrams are strongly linked to the numbers, does Henry move them away from the manipulatives and just use numbers in his teaching practices.
There are many ways that students use the picture grids to express the addition of fractions.
To continue, please open Fun with Picture Grids: Teaching Subtraction
A Math Manipulative to Teach Fractions, © 1993 Speech by Andi Stix, Ed.D.Association of Mathematics Teachers of New York State, Buffalo, NY, ERIC: Eric Resources Information Center #ED408158 (c) 1992 Picture Grids designed by Andi Stix. Produced by ETA/Cuisenaire Company of America. This is the first part of the Fun with Picture Grids Series of Addition, Subtraction, Multiplication & Decimals, Division, and Square Root
————————————–
Andi Stix is an educational consultant & coach who specializes in differentiation, interactive learning, writing across the curriculum, classroom coaching, and gifted education. For further information on her specialties or social media, please email her on the Contact page.
References
Schubert, B. (1987). Mathematics journals: Fourth grade. In Toby Fulwiler (Ed.), The Journal Book. (348-358). Portsmouth, NH Boynton/Cook Publishers.
Stix, Andi N. (1992) .The Development and Field Testing of a Multi-Modal Method for Teaching Mathematical Concepts to Preservice Teachers by Utilizing Pictorial Journal Writing. Ph.D. diss. Columbia University Teachers College. Ann Arbor, MI: U.M.I. Dissertation Information Service, Pub. #92-18719.
Stix, Andi N. (1994). Pictorial journal writing in mathematics. Arithmetic Teacher, 42:1, 264-269.